The method used to claim that there's a cooling trend, or no warming trend, is to cherry-pick a too-recent start year that is exceptionally high and compute the difference between that and a particular recent year (any one, repeat the 'no cooling trend for the last decade' for years afterwards, even if more recent years are warmer).
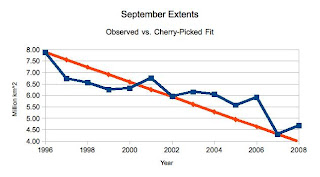
So I'll take a recent year that had large sea ice extent -- 1996, and compute the trend between there and a recent year that had a low extent -- 2007. Here's the straight line computed that way, plotted against the observations between 1996 and present. These data are September ice extents from the NSIDC:
And from eye-inspection of it, it even looks like the average error is about 0. Sometimes high, sometimes low. This trend is for ice pack extent to lose about 330,000 km^2 per year, against the about 78,000 km^2 that is computed for a linear trend by climate scientists. Clearly climate scientists are trying to hide the decline!
I've already done some things more honest than what the 'no warming since 1998' folks do, not least is, I showed you the trend line and the data. But this is far from sufficient to have a reasonable trend analysis.
Not least of the flaws is, most of the data were ignored. Related is, this was too short a period to establish a climate trend. A third is that business about 'average error'.
If I continue the pseudo-skeptics' cherry-picking method, but show you the 'trend' that comes from such an analysis against 30 years of data (1979-2008, this is also the reason for 2008 being the last year shown), the result is:
Now it's clear that this trend computation has nothing to do with representing what's going on with the sea ice extent. If you use a long enough period to be analyzing climate trends, you're protected against several varieties of silly results.
But suppose you are insisting, for some reason, that the climate system changed fundamentally in 1996, so that nothing before then matters. (1998 for those cherry-picking on global temperatures.) Is this trend meaningful then? Well, no.
The problem is the story of the statisticians target shooting. One fired and hit the target a foot to the left of center. The other hit a foot to the right. They then promptly congratulated each other on the fact that on average they had made bullseyes. Here is an example of two lines, both of which have zero average error compared to the observations. If the line is above the data, that's a positive error. If it's below, that's a negative error. We compute the error for every year and add them up. For both lines (the yellow 'least square' line and the orange 'slope-intercept' line) the average is zero.
I repeat: The average is zero. This is why we don't compute trends by looking for a line with zero average error. In fact, there are an infinite number of lines that would have zero average error. Whatever slope you want, I can find an intercept that would give zero average error. Conversely, this is a cherry-picker's dream come true. If they even mention actual numbers, which is rare, they can honestly say that their trend has zero average error. As long as the listeners are sufficient lazy or uninformed, the cherry-pickers are safe.
What is actually done almost all the time in science is to look at the total of the square of the errors. In that case, the fit line being 3 million km^2 too low (a value of -3) becomes and error of 9 (-3 * -3). Later, when the line is 3 million km^2 too high, (a value of +3) the error we add is, again, 9 (3 * 3). The average error for these two is zero. The sum of the squared errors is 18. Big difference! What is normally done is to find the line that has the least squared errors. Also mentioned as 'least squares method', 'least squares fit', 'ordinary least squares', and probably a number of other names. You can get quite a bit more elaborate than this, and at times need to. For such cases, I'll recommend taking a look over at Tamino's place. For instance, his recent article on How not to analyze tide gauge data.
Still, this will give you a decent start in reviewing arguments.
- Trend analysis must be done over a long enough period
- All relevant data should be considered.
- If this results in a period shorter than normally considered long enough, a specific and strong explanation must be made
- Trends cannot be computed by picking a single year to start from and a single end year and then ignore all years in between
- Average error is not sufficient. Squared errors should be used, or some other method which avoids the problems that 'average error' has.
Since I've been mentioning the temperature trends, let's take a look at those. I'll use the Hadley - CRU temperatures because those are favored by the cherry-pickers for this purpose. Others don't show 1998 as the warmest year, which defeats the cherry-picking. Since one of the favorite lines of the cherry-pickers is 'cooling for the last decade', which they've repeated since long after then end of 2007, I'll take the decade 1998-2007. The cherry-pickers' method gives a trend of -0.0147 K per year. If it were meaningful, which a decade isn't for temperature, then that'd be a pretty large figure. Warming over the last century was only around 0.8 K per century, and this would be a cooling of 1.5 K. Least squares over that period shows a warming trend of 0.0046 K per year. Over the century that's about 0.5 K, which is a bit less than the 0.8, but markedly closer. Here's what the two lines look like compared to the data for the 'last decade' of the cherry-pickers:
And here's what it looks like over the whole period of record:
The cherry-pickers' line illustrates two different thing. 1) Why it is we don't use only 10 years to define climate and 2) Why we don't use the cherry pickers' method. Even though 10 years is too short to define climate, if we use least squares, the results are at least not insane.
As usual, don't take my word for any of this. If what I've said is already obvious, I hope you found the writing interesting. If the content is not obvious, get hold of some data yourself, whether the NSIDC (link to the right) ice extents for September, or the HadCRUT (link above) or some other climate data type and start experimenting with the data yourself. Look, yourself, at what kinds of lines you can run through the data, and how long a period you need before the lines start to stabilize -- that one year more or less doesn't mean you need a very different line. Also take a look at methods for finding a line through the data. Average error, I claim, is a very bad method. But try it out yourself. See what happens for least square, least 4th power, least 18th, and so forth.
And, of course, if what you find disagrees with what I've said here, post a comment explaining what you did and how what you saw differs from what I discuss here.
In the mean time, I'll suggest that people applying the cherry-picker method are either not honest -- they're trying to mislead you -- or they just don't know much about how to analyze data. Either way, these aren't the people to learn about climate from, no matter how much you might like their thoughts and conclusions. That's one of the drawbacks to doing science -- the people doing the best work aren't always the ones you like the most.
Update (3 Aug 2011): It seems that blogger is having problems with comments. That's particularly unfortunate here as I think there are likely many good comments getting choked by the system. If you've had this problem, please email them to me at bobg at radix dot net.







8 comments:
Hi Bob,
I'm glad you're blogging again and assigning homework.
I tried the links to the Excel and Openoffice files and get a blogger sign in page that does not take me anywhere. Could you confirm that the files are available?
thanks,
jg
Oops. Links are live now.
I think of it more as inviting people to join the game than assigning homework. :-)
Thanks Bob,
I was able to open the file and I found it instructive just to see how you set up the formulae.
jg
I see the "random walk" assertion popping up again; will you comment? Here's a couple:
http://pielkeclimatesci.wordpress.com/2011/02/14/new-paper-random-walk-lengths-of-about-30-years-in-global-climate-by-bye-et-al-2011/
http://ocham.blogspot.com/2011/07/global-warming-random-walks.html
Hank:
I'll see about getting the paper that Pielke links to -- Bye, J., K. Fraedrich, E. Kirk, S. Schubert, and X. Zhu (2011), Random walk lengths of about 30 years in global climate, Geophys. Res. Lett., doi:10.1029/2010GL046333, in press. (accepted 7 February 2011)
Fraedrich is someone whose work I've seen before, favorably. It'll be interesting to see how much they push a conclusion of "it's all noise" as opposed to merely supporting in a very different way my conclusion that if you want to talk about climate, you need 30 years of data.
Robert, I'm uncomfortable with the literary device you use of refuting an imaginary (and apparently idiotic) opponent. I don't know anyone who thinks that the 1998 spike in global average temperature was due to anything but an El Nino event.
Eliot:
Suppose that the opponent really is imaginary. Does that change the merit in _not_ cherry picking short periods over which to compute climate trends?
Sadly, however, there are indeed people who select 1998 as the starting point for their comments, and did so with even shorter records. See, for example:
http://www.telegraph.co.uk/comment/personal-view/3624242/There-IS-a-problem-with-global-warming...-it-stopped-in-1998.html
http://www.prisonplanet.com/articles/june2007/180607_b_Climate.htm
http://blogs.wsj.com/iainmartin/2009/10/12/bbc-global-warming-stopped-in-1998/
http://www.uncommondescent.com/off-topic/scientist-says-global-warming-stopped-in-1998/
http://boards.straightdope.com/sdmb/showthread.php?t=370001
http://hot-topic.co.nz/john-im-only-dancing/
And, from only a couple weeks ago:
http://www.businessinsider.com/what-ever-happened-to-global-warming-2011-7
Or 4 days ago:
http://www.thestarphoenix.com/technology/real+scandal/5182959/story.html
You can also pursue it readily by selectively searching just on news articles, or just on blogs, as opposed to general web searches. Or, for that matter, books:
http://books.google.com/books?id=OOgV_Eu-ASAC&lpg=PA476&dq=warming%20stopped%20in%201998%20-%22bob%20carter%22&pg=PA477#v=onepage&q=warming%20stopped%20in%201998%20-%22bob%20carter%22&f=false
-- where they do recognize 1998 as an outlier El Nino year, and instead cherry-pick the even shorter period of 2001-2007.
How you describe those authors, and the thousands who have repeated their arguments, is your call. But they do indeed exist. My literary illustration was straight from reality, not my creativity.
Actually, I think that the data shows the opposite of what you conclude. I would say that something happened circa 1996 to cause sea ice extent to decrease at a higher rate than pre-1996. The low extent observed in 2011 is real, and not a statistical quirk. The value of September Sea ice extent will be about 4 million km2, not 7 million km2 as you would expect from the long term average.
Post a Comment