I'll fling this open for comment, and hold mine for later so as to not steer things too much. What is scientific literacy? There's enough talk publicly about there not being enough scientific literacy around, and I tend to agree, but I've noticed that it's pretty rare for anybody to say just what they mean by the term. Maybe I wouldn't agree if I knew what they meant.
What are your thoughts on what scientific literacy is? And how important (please compare it to something else, not just 'very', or 'hardly at all') do you think it is for modern societies to be scientifically literate?
28 July 2009
27 July 2009
How not to analyze climate data
Preface
The paper that prompts this post (and the preceding Introduction to time series analysis is McLean, de Freitas, and Carter, 2009. A reader suggested, in email, that I take a look. I'll recommend that to others as well. I won't carry out all suggestions, not least because I don't know all areas well enough to comment, but they are indeed welcome. And do at times result in a post here. There'll be some following notes as this paper opens several issues. For now, I'll stay with just the paper.
Comments have already appeared at OpenMind, Initforthegold, and Realclimate. In a fundamental sense, I won't be adding anything new. But the approach will differ and might show some features in ways that you might have missed in the comments over there. For instance, I mentioned the crucial bit that I'll be exploring here in a comment at Initforthegold, and Michael missed its significance on first reading. The fundamental was staring him in the face, but fundamentals aren't always easy to notice. When he did, it was 'forehead slap' time.
I've tagged this 'doing science' and 'weeding sources', as well as 'climate change'. Some issues of peer review will show up, as will a flag or two of mine which I find useful in weeding sources. The nominal topic of the paper "Influence of the Southern Oscillation on tropospheric temperature" is climate change. Recently I posted about scientific specificity. While it's entirely true that it doesn't work well to take that line in daily life, it's exactly what one should do with a scientific paper. One thing it means is that we keep an eye on whether the data used, or are used, support the argument that is made.
Begin
We start by reading the abstract. As a matter of doing science, the abstract usually makes the most eye-catching statements in the paper. It is the advertising section of the paper, so to speak. You want to say something here that will interest other scientists and get them to read your brilliant work. In this case, "That mean global tropospheric temperature has for the last 50 years fallen and risen in close accord with the SOI of 5–7 months earlier shows the potential of natural forcing mechanisms to account for most of the temperature variation."
SOI is the Southern Oscillation Index. It provides a number that is connected to the El Nino-Southern Oscillation (ENSO), which can then be used for further research, such as this paper. There are different ways of defining an SOI, which might be an issue if the effects the authors were working with were fairly subtle. But, as they are referring to explaining 68-81% of the variance (figure depends on which records are matched, and how large the domain examined is), we've left the realm of subtle. As the authors duly cite, there's nothing new in seeing a correlation between SOI and global mean temperatures. This is well-known. What is new is the extraordinarily high correlations they find, and that eye-catching conclusion that most of temperature variation for the last 50 years is driven by SOI.
For atmospheric temperatures, they use the UAH lower tropospheric sounding temperatures (paragraph 5) and for SOI, they use the Australian Bureau of Meteorology's index (para 7). If the abstract were an accurate guide, we'd expect that with those two time series in hand, they computed the correlations and found those very high percentages of variance explained. Or at least that they were that high with the noted 5-7 month lag. And here's where we get to the time series analysis issue that I was introducing Friday.
Three different things are done to the data sets before computing the correlations. One is to exclude certain time spans for being contaminated by volcanic effects on the temperatures. No particular time series analysis issue here. But the other two both have marked effects on time series. First (para 10) is to perform a 12 month running average. This, as I discussed Friday, mostly suppresses effects that are 1 year and shorter in period. Second is to take the difference between those means, 12 months apart (paragraph 14). As I described on Friday, this suppresses long term variation, and enhances short term variation. They assert that this removes noise, while, in fact, it amplifies noise (high frequency/short period components of the record). Alternately, they are defining 'noise' to be the long period part of the records -- the climate portion of the record.
The combined effect of the two filters is that both the high frequency and the low frequency parts of the records are suppressed. What is left is whatever portion of the two records lie in the mid-range frequencies. To return to my music analogies, what has been done is to set your equalizer in a V shape, with the highest amplitudes in mid-range. While the result has a connection to the original data, it is certainly no longer fair to say, as the authors do in the abstract, that their correlations are between SOI and temperatures.
Demonstration of filter effects -- sample series
The next 4 figures show k) the original time series, which I constructed by adding up some simple periodic functions l) the 12 month running average version m) the 12 month differencing of the original data and n) applying both filters as the authors did (minus volcanoes).
Original

12 Month Smoothing

12 Month Differencing

Both Filters
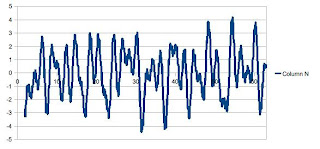
As expected, the running average smoothed out the series. In music terms, it suppressed the treble. That's the job of an averaging filter. The differencing made for a much choppier series than the original. That, too, can be desirable. But certainly the authors' comment about 'removing noise' is ill-founded. If we look at the variance in the time series, the original has a variance of 4.25. The running average decreased that to 2.69 (eliminating 37% of the variance). The differencing increased the variance 50%, to 6.47 (again, increased variance means more noise). Applying both filters produces the final figure, which has little resemblance to the original series. Not least, while the original looks to have a substantial amplitude at a period of 30 years (that appearance is entirely correct, I put in a 30 year period), the final product shows no sign whatever of the 30 year period. That is one of the jobs of a differencing filter -- remove the long period contributions. The filters have also suppressed the 15 year period that I put in, and, in general, turned my original series, which had equal contributions at 5 months, 1, 2, 3, 5, 7, 10, 15, 30 years into something that looks mostly like a 3 year period (count the peaks and divide that in to the time span for them) with a bit of noise.
Filter effects on SOI series
That was a warm up with a test series, where we know that there are no data problems of any sort, and we know exactly what went in. The real data of course have problems (this is always true, and one of the aspects of doing science), but they may not have problems that affect our conclusions. The next figure shows the smoothed (12 month running averages again) and then differenced (as in the paper) Australian SOI (labelled 'both' -- both the averaging and the differencing applied to the original data) (Note that I'm not showing the full curve, only 1950 to present, instead of 1879 to present -- the paper's analyses only covered, at most, 1958-2008).

You see that with both filters applied there are new peaks, missing peaks, and even the sign of the index can change (positive for negative, or vice versa). These are all signs that the filters have fundamentally altered the data set, so that whatever conclusion is drawn can only be drawn about 'data as processed by this filter', not the original data -- in contradiction to the statements in the paper and elsewhere by the authors that it is SOI that explains an extremely high portion of the variation in global mean temperature. Further, since the correlation is largely driven by the peaks, the high correlations can by largely a matter of how the filter creates or destroys peaks rather than the underlying data.
Response function
I mentioned Friday the amplitude spectrum -- show the amplitudes of the contributions from each period. Filters change the amplitude spectrum. That's their job. One thing, then, that you do to describe the filter is divide the amplitude at a period after processing with the amplitude before hand (this is known as the response function). An ideal filter will show a 1 for all periods except the ones you're trying to get rid of, where it will be 0. Real filters don't accomplish this, but that's the goal. So, to see the performance of the author's filter, I took their original SOI series, processed it through their filter, and then found the response function in this way. Those are the next figures. First is looking at cycles per year (frequency), letting us see well what happens at high frequencies. Second looks at the period (from 1-15 years).
Frequency Response Function
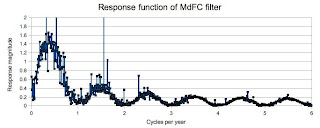
Period Response Function

There are some spikes in the curves, which have nothing to do with the filter. All that is happening there is the these are periods/frequencies which have little signal in the original series, so numerical processing issues can have large effects there (dividing by small numbers is hazardous). But the smooth curve is a fair description. The averaging filter suppresses the signal (response is close to 0) for frequencies of 1, 2, 3, 4, 5, 6 cycles per year. (With monthly data, 6 cycles per year is the highest that can be analyzed -- 2 months period.). The differencing filter also suppresses the very low frequencies (long periods), as we expected even with just the basic introduction from Friday. But take a look between 1.5 and 7 years. The response is greater than the input! Look, too, at the periods which are being amplified. A usual description of ENSO is 'an oscillation with a period of 3-7 years'.
Summary
So what do we really have? It isn't a correlation between SOI and global mean temperatures. Both were heavily filtered. What the authors actually compute is the correlation between the SOI time series and global mean temperature -- if you over-weight (response function is greater than 1, so it's an over-weighting) both series towards what is happening in the ENSO periods. The conclusion should really be "If you look only in the ENSO window, you see that ENSO accounts for a lot of variation in global mean temperature." One problem is, that isn't a new result. We already knew that ENSO was important in the ENSO periods. More important to the paper, in so doing, the authors cannot make any conclusion about explaining "most of the temperature variation". They've filtered out much of it, and never examined either the response function nor the effects of their filter on the inputs.
If what was desired was an analysis of global mean temperature response to SOI at ENSO periods, then both the authors should have been clear that this was their window, and they should have used a more suitable filtering process. When one goes back to the paper, it's also clear that no justification was ever made for using either filter, much less both. The filters were arbitrary, and as I've mentioned, we prefer to avoid arbitrary decisions in our papers. If no objective basis for setting up the filters could be found, the authors should have demonstrated that alternate choices did not affect their conclusions.
So, some 'weeding sources', or 'scientific specificity' signs:
* When a paper makes a conclusion about the correlation between A and B, verify that it is A and B that they are correlating.
* If a filter is applied, look for the authors to discuss a) why a filter is being applied at all, and b) why the particular filter they chose was used.
As is my custom, I've sent an email to one of the authors (de Freitas, the only one whose email was given in the paper) about this comment.
Some of the following blog posts will talk about the peer-review aspects that let this paper through. For now, see my old article peer review. One of the other notes (no idea when) will be about how the process continues after a bad paper gets through the peer review process. That is the comment and reply process, and I'll be writing Tamino about that (he's said in his comments that he's preparing a comment for the journal).
The paper that prompts this post (and the preceding Introduction to time series analysis is McLean, de Freitas, and Carter, 2009. A reader suggested, in email, that I take a look. I'll recommend that to others as well. I won't carry out all suggestions, not least because I don't know all areas well enough to comment, but they are indeed welcome. And do at times result in a post here. There'll be some following notes as this paper opens several issues. For now, I'll stay with just the paper.
Comments have already appeared at OpenMind, Initforthegold, and Realclimate. In a fundamental sense, I won't be adding anything new. But the approach will differ and might show some features in ways that you might have missed in the comments over there. For instance, I mentioned the crucial bit that I'll be exploring here in a comment at Initforthegold, and Michael missed its significance on first reading. The fundamental was staring him in the face, but fundamentals aren't always easy to notice. When he did, it was 'forehead slap' time.
I've tagged this 'doing science' and 'weeding sources', as well as 'climate change'. Some issues of peer review will show up, as will a flag or two of mine which I find useful in weeding sources. The nominal topic of the paper "Influence of the Southern Oscillation on tropospheric temperature" is climate change. Recently I posted about scientific specificity. While it's entirely true that it doesn't work well to take that line in daily life, it's exactly what one should do with a scientific paper. One thing it means is that we keep an eye on whether the data used, or are used, support the argument that is made.
Begin
We start by reading the abstract. As a matter of doing science, the abstract usually makes the most eye-catching statements in the paper. It is the advertising section of the paper, so to speak. You want to say something here that will interest other scientists and get them to read your brilliant work. In this case, "That mean global tropospheric temperature has for the last 50 years fallen and risen in close accord with the SOI of 5–7 months earlier shows the potential of natural forcing mechanisms to account for most of the temperature variation."
SOI is the Southern Oscillation Index. It provides a number that is connected to the El Nino-Southern Oscillation (ENSO), which can then be used for further research, such as this paper. There are different ways of defining an SOI, which might be an issue if the effects the authors were working with were fairly subtle. But, as they are referring to explaining 68-81% of the variance (figure depends on which records are matched, and how large the domain examined is), we've left the realm of subtle. As the authors duly cite, there's nothing new in seeing a correlation between SOI and global mean temperatures. This is well-known. What is new is the extraordinarily high correlations they find, and that eye-catching conclusion that most of temperature variation for the last 50 years is driven by SOI.
For atmospheric temperatures, they use the UAH lower tropospheric sounding temperatures (paragraph 5) and for SOI, they use the Australian Bureau of Meteorology's index (para 7). If the abstract were an accurate guide, we'd expect that with those two time series in hand, they computed the correlations and found those very high percentages of variance explained. Or at least that they were that high with the noted 5-7 month lag. And here's where we get to the time series analysis issue that I was introducing Friday.
Three different things are done to the data sets before computing the correlations. One is to exclude certain time spans for being contaminated by volcanic effects on the temperatures. No particular time series analysis issue here. But the other two both have marked effects on time series. First (para 10) is to perform a 12 month running average. This, as I discussed Friday, mostly suppresses effects that are 1 year and shorter in period. Second is to take the difference between those means, 12 months apart (paragraph 14). As I described on Friday, this suppresses long term variation, and enhances short term variation. They assert that this removes noise, while, in fact, it amplifies noise (high frequency/short period components of the record). Alternately, they are defining 'noise' to be the long period part of the records -- the climate portion of the record.
The combined effect of the two filters is that both the high frequency and the low frequency parts of the records are suppressed. What is left is whatever portion of the two records lie in the mid-range frequencies. To return to my music analogies, what has been done is to set your equalizer in a V shape, with the highest amplitudes in mid-range. While the result has a connection to the original data, it is certainly no longer fair to say, as the authors do in the abstract, that their correlations are between SOI and temperatures.
Demonstration of filter effects -- sample series
The next 4 figures show k) the original time series, which I constructed by adding up some simple periodic functions l) the 12 month running average version m) the 12 month differencing of the original data and n) applying both filters as the authors did (minus volcanoes).




As expected, the running average smoothed out the series. In music terms, it suppressed the treble. That's the job of an averaging filter. The differencing made for a much choppier series than the original. That, too, can be desirable. But certainly the authors' comment about 'removing noise' is ill-founded. If we look at the variance in the time series, the original has a variance of 4.25. The running average decreased that to 2.69 (eliminating 37% of the variance). The differencing increased the variance 50%, to 6.47 (again, increased variance means more noise). Applying both filters produces the final figure, which has little resemblance to the original series. Not least, while the original looks to have a substantial amplitude at a period of 30 years (that appearance is entirely correct, I put in a 30 year period), the final product shows no sign whatever of the 30 year period. That is one of the jobs of a differencing filter -- remove the long period contributions. The filters have also suppressed the 15 year period that I put in, and, in general, turned my original series, which had equal contributions at 5 months, 1, 2, 3, 5, 7, 10, 15, 30 years into something that looks mostly like a 3 year period (count the peaks and divide that in to the time span for them) with a bit of noise.
Filter effects on SOI series
That was a warm up with a test series, where we know that there are no data problems of any sort, and we know exactly what went in. The real data of course have problems (this is always true, and one of the aspects of doing science), but they may not have problems that affect our conclusions. The next figure shows the smoothed (12 month running averages again) and then differenced (as in the paper) Australian SOI (labelled 'both' -- both the averaging and the differencing applied to the original data) (Note that I'm not showing the full curve, only 1950 to present, instead of 1879 to present -- the paper's analyses only covered, at most, 1958-2008).

You see that with both filters applied there are new peaks, missing peaks, and even the sign of the index can change (positive for negative, or vice versa). These are all signs that the filters have fundamentally altered the data set, so that whatever conclusion is drawn can only be drawn about 'data as processed by this filter', not the original data -- in contradiction to the statements in the paper and elsewhere by the authors that it is SOI that explains an extremely high portion of the variation in global mean temperature. Further, since the correlation is largely driven by the peaks, the high correlations can by largely a matter of how the filter creates or destroys peaks rather than the underlying data.
Response function
I mentioned Friday the amplitude spectrum -- show the amplitudes of the contributions from each period. Filters change the amplitude spectrum. That's their job. One thing, then, that you do to describe the filter is divide the amplitude at a period after processing with the amplitude before hand (this is known as the response function). An ideal filter will show a 1 for all periods except the ones you're trying to get rid of, where it will be 0. Real filters don't accomplish this, but that's the goal. So, to see the performance of the author's filter, I took their original SOI series, processed it through their filter, and then found the response function in this way. Those are the next figures. First is looking at cycles per year (frequency), letting us see well what happens at high frequencies. Second looks at the period (from 1-15 years).


There are some spikes in the curves, which have nothing to do with the filter. All that is happening there is the these are periods/frequencies which have little signal in the original series, so numerical processing issues can have large effects there (dividing by small numbers is hazardous). But the smooth curve is a fair description. The averaging filter suppresses the signal (response is close to 0) for frequencies of 1, 2, 3, 4, 5, 6 cycles per year. (With monthly data, 6 cycles per year is the highest that can be analyzed -- 2 months period.). The differencing filter also suppresses the very low frequencies (long periods), as we expected even with just the basic introduction from Friday. But take a look between 1.5 and 7 years. The response is greater than the input! Look, too, at the periods which are being amplified. A usual description of ENSO is 'an oscillation with a period of 3-7 years'.
Summary
So what do we really have? It isn't a correlation between SOI and global mean temperatures. Both were heavily filtered. What the authors actually compute is the correlation between the SOI time series and global mean temperature -- if you over-weight (response function is greater than 1, so it's an over-weighting) both series towards what is happening in the ENSO periods. The conclusion should really be "If you look only in the ENSO window, you see that ENSO accounts for a lot of variation in global mean temperature." One problem is, that isn't a new result. We already knew that ENSO was important in the ENSO periods. More important to the paper, in so doing, the authors cannot make any conclusion about explaining "most of the temperature variation". They've filtered out much of it, and never examined either the response function nor the effects of their filter on the inputs.
If what was desired was an analysis of global mean temperature response to SOI at ENSO periods, then both the authors should have been clear that this was their window, and they should have used a more suitable filtering process. When one goes back to the paper, it's also clear that no justification was ever made for using either filter, much less both. The filters were arbitrary, and as I've mentioned, we prefer to avoid arbitrary decisions in our papers. If no objective basis for setting up the filters could be found, the authors should have demonstrated that alternate choices did not affect their conclusions.
So, some 'weeding sources', or 'scientific specificity' signs:
* When a paper makes a conclusion about the correlation between A and B, verify that it is A and B that they are correlating.
* If a filter is applied, look for the authors to discuss a) why a filter is being applied at all, and b) why the particular filter they chose was used.
As is my custom, I've sent an email to one of the authors (de Freitas, the only one whose email was given in the paper) about this comment.
Some of the following blog posts will talk about the peer-review aspects that let this paper through. For now, see my old article peer review. One of the other notes (no idea when) will be about how the process continues after a bad paper gets through the peer review process. That is the comment and reply process, and I'll be writing Tamino about that (he's said in his comments that he's preparing a comment for the journal).
Labels:
climate change,
doing science,
weeding sources
24 July 2009
Introductory Time Series Analysis
As often happens, this note is prompted by someone doing things that look wrong. Time series analysis is something which has been an interest of mine since I earned my Master's (looking at tidal signals in current meter data). And there are some elements which I think are eminently understandable without diving in to the gory details. So here is my shot at a very short, only marginally mathematical, introduction to time series analysis.
A time series is just a series of observations (of something, anything) through time. The monthly averaged global mean temperatures that I use for demonstrating principles of climate are time series. Monthly Southern Oscillation Index is another time series. Not coincidentally, those are the ones examined in the paper, and are what I'll consider here. But there are innumerable other time series -- daily close of the stock exchange, daily temperature, your weight day by day, and so on.
Much of the language for talking about time series is fairly ordinary. But there are a few terms I'd like to be sure we're using the same. Most important is 'period'. The period of something in your time series is the length of time from peak to peak (or trough to trough). Consider hourly temperatures in your area. They peak each day, around, say 3 PM. The period is then 24 hours. If we take a longer view, and consider daily high temperature, then the temperatures peak each year -- a period of 1 year. If we think of the brightness of the moon, it has a period (full moon to full moon) of 29.53 days. And so on. We could also ask how often the peak occurred per year (or other time of interest). This is the frequency -- how frequently do you hit the peaks. For hourly temperatures, the frequency is 365 per year (or 365 cycles per year). The frequency of the lunar cycle is 12.369 cycles per year. And the seasonal cycle has a frequency of 1 cycle per year.
In talking about periods and frequencies, and scientists tend to use the two terms interchangeably since the value of one can always be converted to a value of the other, we sometimes also hear about long/short periods, or high/low frequency. In the periods, it means what ordinary english would lead you to think -- long periods are periods that take a long time from peak to peak, and short periods are fast from peak to peak. You still have to know what is 'long' for the system to read any given paper correctly. If it's a geologist, they could mean 400 million years when they say 'long period' (the period for continental drift cycling), where a meteorologist might mean 40 years. High frequencies correspond to short periods (since the period is short, the thing happens often -- at high frequency). Low frequencies have long periods. The similarity of term with music is no accident. Low frequency sound (low pitch) has a long period, while high frequency sound has a short period.
So when you hit anything relating to time series, if you know about music, think in terms of frequencies and pitches. Another term that comes up in time series analysis, with a slightly different meaning than in music, is 'harmonic'. Unlike music, with its fifths, thirds, etc., in time series we work more simply. There is the base period/frequency. And then there are the integral multiples of that base frequency. The annual cycle's harmonics are 1 (the base period), 2 (6 month period, 2 cycles per year), 3 (4 month period, 3 cycles per year), 4 (you get the idea), and higher. In practice much of our weather time series can be captured by the first 4 harmonics of the annual cycle. (That's interesting in its own right -- it means that there is relatively little happening at periods of 5, 7, 8, 9 months, even though there's a lot at 4, 6, 12 months.)
As with music, we also are interested in how loud the frequency is. Our measure there is called amplitude. It is half the distance from peak to trough. Where I live, our peak summer high temperatures are about 90 F (32 C), and in the winter, our lowest highs are about ... call it -10 C (14 F). The range is 42 C, so the amplitude of our seasonal cycle is 21 C.
Again following music, there's usually more than one frequency being played at a time. This is certainly true for weather! Many different things happening all the time. In music, the description of all the notes the band or orchestra are playing at a time is called the score. For time series analysis, it is the spectrum. A little more involved in time series because we can look at different spectra (1 spectrum, 2 or more spectra) -- the amplitude spectrum, and the 'power' spectrum. Most work is actually done with the power spectrum, but the amplitude spectrum is easier to understand so I'll stay with that.
One of the things we do in looking at climate time series is average the data -- construct a moving average, for instance. The moving average says to take the first (some number, let's say 12) months of data and average them together. Then step forward (move) 1 month, and average the next 12. Repeat until you're at the last 12 months of data. As I've suggested for understanding global climate, you want quite a bit more than 12 months of data in your averaging. But we can also try to understand weather. A 12 month average will clobber most of what is happening shorter than 12 month periods (but not absolutely all of it, a point even scientists seem to forget -- it only completely clobbers the 12 month period and its harmonics), and let us look at what is happening on periods longer than 12 months (but some of that, too, gets damped). In musical terms, averaging suppresses the high notes, while leaving the bass line relatively unaffected.
Suppose what we really want is to suppress the bass line and enhance the treble -- suppress the climate frequencies and focus on the weather. Rather than averaging, which is a smoothing operation that suppresses the high frequencies, we would take differences. Say take the difference between months 12 months apart. We can think of the temperature as being a certain amount of weather, plus a certain amount of climate. The climate will be nearly the same 12 months apart, so when we do the subtraction, it is cancelled out and we have only the difference in weather those two months. Differencing is a sharpening operation that suppresses the bass line and enhances the treble. It is, however, an extremely biased operation -- not only does it suppress some and enhance others, but the degree of enhancement is proportional to the frequency. Unlike the averaging operation, which leaves low enough frequencies unchanged, the differencing affects all frequencies and does so strongly.
Changing time series data is called a filtering. The averaging and differencing operations are different filters. There are many, many more that we could use. Any time we do use a filter, though, we should be careful that it isn't creating problems for us. This is one reason I try always to work with the most nearly original data possible -- no filtering has been done that could obscure the effects I'm trying to work with.
If you're a more visual person than a music person, the spectrum (guess where we stole that word from!) also has some color traits. If the amplitudes are all about the same, regardless of the frequency, then we call it a 'white' spectrum. (White light is approximately equal contributions of all colors.) Instead of period, for light we think of wavelength. Frequency is still frequency, but now it means how many times per meter you see the peaks. High frequency light is blue. Low frequency light is red. When we do the moving average, we are making the spectrum redder. When we do a differencing, we are making the spectrum bluer. Most climate-related time series have red spectra -- there are higher amplitudes at longer periods (wavelengths). Our year to year variations are on the order of 0.1 C, but the ice age cycles are 5 C, for instance.
A time series is just a series of observations (of something, anything) through time. The monthly averaged global mean temperatures that I use for demonstrating principles of climate are time series. Monthly Southern Oscillation Index is another time series. Not coincidentally, those are the ones examined in the paper, and are what I'll consider here. But there are innumerable other time series -- daily close of the stock exchange, daily temperature, your weight day by day, and so on.
Much of the language for talking about time series is fairly ordinary. But there are a few terms I'd like to be sure we're using the same. Most important is 'period'. The period of something in your time series is the length of time from peak to peak (or trough to trough). Consider hourly temperatures in your area. They peak each day, around, say 3 PM. The period is then 24 hours. If we take a longer view, and consider daily high temperature, then the temperatures peak each year -- a period of 1 year. If we think of the brightness of the moon, it has a period (full moon to full moon) of 29.53 days. And so on. We could also ask how often the peak occurred per year (or other time of interest). This is the frequency -- how frequently do you hit the peaks. For hourly temperatures, the frequency is 365 per year (or 365 cycles per year). The frequency of the lunar cycle is 12.369 cycles per year. And the seasonal cycle has a frequency of 1 cycle per year.
In talking about periods and frequencies, and scientists tend to use the two terms interchangeably since the value of one can always be converted to a value of the other, we sometimes also hear about long/short periods, or high/low frequency. In the periods, it means what ordinary english would lead you to think -- long periods are periods that take a long time from peak to peak, and short periods are fast from peak to peak. You still have to know what is 'long' for the system to read any given paper correctly. If it's a geologist, they could mean 400 million years when they say 'long period' (the period for continental drift cycling), where a meteorologist might mean 40 years. High frequencies correspond to short periods (since the period is short, the thing happens often -- at high frequency). Low frequencies have long periods. The similarity of term with music is no accident. Low frequency sound (low pitch) has a long period, while high frequency sound has a short period.
So when you hit anything relating to time series, if you know about music, think in terms of frequencies and pitches. Another term that comes up in time series analysis, with a slightly different meaning than in music, is 'harmonic'. Unlike music, with its fifths, thirds, etc., in time series we work more simply. There is the base period/frequency. And then there are the integral multiples of that base frequency. The annual cycle's harmonics are 1 (the base period), 2 (6 month period, 2 cycles per year), 3 (4 month period, 3 cycles per year), 4 (you get the idea), and higher. In practice much of our weather time series can be captured by the first 4 harmonics of the annual cycle. (That's interesting in its own right -- it means that there is relatively little happening at periods of 5, 7, 8, 9 months, even though there's a lot at 4, 6, 12 months.)
As with music, we also are interested in how loud the frequency is. Our measure there is called amplitude. It is half the distance from peak to trough. Where I live, our peak summer high temperatures are about 90 F (32 C), and in the winter, our lowest highs are about ... call it -10 C (14 F). The range is 42 C, so the amplitude of our seasonal cycle is 21 C.
Again following music, there's usually more than one frequency being played at a time. This is certainly true for weather! Many different things happening all the time. In music, the description of all the notes the band or orchestra are playing at a time is called the score. For time series analysis, it is the spectrum. A little more involved in time series because we can look at different spectra (1 spectrum, 2 or more spectra) -- the amplitude spectrum, and the 'power' spectrum. Most work is actually done with the power spectrum, but the amplitude spectrum is easier to understand so I'll stay with that.
One of the things we do in looking at climate time series is average the data -- construct a moving average, for instance. The moving average says to take the first (some number, let's say 12) months of data and average them together. Then step forward (move) 1 month, and average the next 12. Repeat until you're at the last 12 months of data. As I've suggested for understanding global climate, you want quite a bit more than 12 months of data in your averaging. But we can also try to understand weather. A 12 month average will clobber most of what is happening shorter than 12 month periods (but not absolutely all of it, a point even scientists seem to forget -- it only completely clobbers the 12 month period and its harmonics), and let us look at what is happening on periods longer than 12 months (but some of that, too, gets damped). In musical terms, averaging suppresses the high notes, while leaving the bass line relatively unaffected.
Suppose what we really want is to suppress the bass line and enhance the treble -- suppress the climate frequencies and focus on the weather. Rather than averaging, which is a smoothing operation that suppresses the high frequencies, we would take differences. Say take the difference between months 12 months apart. We can think of the temperature as being a certain amount of weather, plus a certain amount of climate. The climate will be nearly the same 12 months apart, so when we do the subtraction, it is cancelled out and we have only the difference in weather those two months. Differencing is a sharpening operation that suppresses the bass line and enhances the treble. It is, however, an extremely biased operation -- not only does it suppress some and enhance others, but the degree of enhancement is proportional to the frequency. Unlike the averaging operation, which leaves low enough frequencies unchanged, the differencing affects all frequencies and does so strongly.
Changing time series data is called a filtering. The averaging and differencing operations are different filters. There are many, many more that we could use. Any time we do use a filter, though, we should be careful that it isn't creating problems for us. This is one reason I try always to work with the most nearly original data possible -- no filtering has been done that could obscure the effects I'm trying to work with.
If you're a more visual person than a music person, the spectrum (guess where we stole that word from!) also has some color traits. If the amplitudes are all about the same, regardless of the frequency, then we call it a 'white' spectrum. (White light is approximately equal contributions of all colors.) Instead of period, for light we think of wavelength. Frequency is still frequency, but now it means how many times per meter you see the peaks. High frequency light is blue. Low frequency light is red. When we do the moving average, we are making the spectrum redder. When we do a differencing, we are making the spectrum bluer. Most climate-related time series have red spectra -- there are higher amplitudes at longer periods (wavelengths). Our year to year variations are on the order of 0.1 C, but the ice age cycles are 5 C, for instance.
23 July 2009
Coming attractions
Tomorrow I'll be introducing time series analysis. This is prompted in part by a reader who asked me to comment on a paper that just came out, and partly because it's an interest of mine. After that (not sure of date because I'll have to do some data analysis and plotting for you), I'll take up the paper, from the standpoint of the simple sorts of time series analysis considerations I outline tomorrow.
In the mean time, if you haven't looked in on the comments lately, particularly in the 'communicating science' threads, please do. Some good thoughts there.
Also, changing topics: About a year ago, when I was starting to post regularly, some more popular blogs mentioned mine. So, my turn now to mention Kate at http://climatesight.org/
In the mean time, if you haven't looked in on the comments lately, particularly in the 'communicating science' threads, please do. Some good thoughts there.
Also, changing topics: About a year ago, when I was starting to post regularly, some more popular blogs mentioned mine. So, my turn now to mention Kate at http://climatesight.org/
21 July 2009
Timelines
Some ages ago, I assembled time lines. Seeing JG's much better timelines (and with live content, vs. my static listing) reminded me of them. One feature of my approach was to use a set of time lines, each of which was about 10 times shorter than the previous. That number varied widely in practice. But the basic idea was to take a look over time to the present, focusing more and more narrowly towards the present.
I did this so long ago that a number of dates need to be changed -- the universe is 13.7 billion years old, not the 15 that I used, for instance. Still, here's a look at the version of my timelines from 10 years ago, from shortest to longest periods. Maybe I can entice JG to using this idea for his version?
In any case, enjoy. When you see things that are dated wrong, or see important things that should be added, do comment. (There's no question of if; even my casual glances were showing a lot of things in need of update and addition or deletion.)








I did this so long ago that a number of dates need to be changed -- the universe is 13.7 billion years old, not the 15 that I used, for instance. Still, here's a look at the version of my timelines from 10 years ago, from shortest to longest periods. Maybe I can entice JG to using this idea for his version?
In any case, enjoy. When you see things that are dated wrong, or see important things that should be added, do comment. (There's no question of if; even my casual glances were showing a lot of things in need of update and addition or deletion.)
20 July 2009
What cooling trend?
Nonsense about the 'current cooling trend' is rife across the blogosphere, and the science minded folks usually point to the fact that you need 20-30 years to define a climate trend. The lies as such don't interest me, or make for a good topic for this blog.
What's useful or interesting is that the statement itself, often linked to 'last 10 years', is not true even after allowing for substantial cherry picking. This brings us back to the interesting matter of trying to define climate. And a further reminder that if you're reading bad sources, you can't trust even the simplest of statements.
To find current temperature trends, I used the NCDC monthly temperature anomalies. The most recent month is May, 2009. To look in to current trends, then, I computed the trends from every month of the last 30 years, through to May 2009. The trend shown for January 1979 is the trend from then to May 2009. The trend for April 2009 is to May 2009. Figure 1 gives the results (actually back to 1977).

Wow, current warming trend of 120 C per century! Surely we're all going to be boiling soon? Of course not. That trend was computed from a 1 month span -- April to May of 2009. It is yet another reminder that short term variations, namely weather, can be large. It isn't climate. Climate shouldn't depend sensitively on when exactly you start your trend computation. Unfortunately that figure shows us nothing new, beyond confirming yet again (not a bad process itself, and part of the scientific approach) that weather happens, and weather variability is much larger than climate variability. So in figure 2, I zoom in a little and ignore positive trends greater than 20 C/century.

So now we can see that if someone chooses very carefully (namely, cherry picks) the starting date, they can find a cooling trend between then and May 2009 ('current'). But notice how carefully they have to choose that starting date. If it's 10 years (or any number greater than that, back to the record's start date), the trend is a warming. In fact, you can only get cooling trends occur if you choose a start date between January 2001 and January 2007 (including those months), or October, 2008. Anything farther back, or more recent, shows warming.
Both for deciding climate, and for doing science, we want our conclusions not to depend sensitively on arbitrary choices. Ending with the most recent data is not arbitrary, so we're ok there. But choosing a starting date? Science-minded folks take a figure in the range of 20-30 years, in particular 30, because over a century of experience says that 30 years is a good time period to be able to look at climate trends as opposed to weather fluctuations. i.e., not arbitrary. Choosing 2.4-8.4 years (and not 9.4, or 12, ...)? Why would we do that? Well, if we wanted to support some particular conclusion, we might do so. But that is not science.
Let's zoom our attention to the period in late 2006 through early 2007. The largest 'cooling trend' you can contrive is to start with September or October 2006, giving 3.3 C per century cooling. Of course you're flagrantly violating sensible climate practice by using 30 months instead of 30 years. But now look to April 2007, where the trend is already a warming of 3.3 C/century, and remains higher than 3.3 to the present, except for that 1 month, October 2008. If 30 months are ok for cherry pickers, why are 24 months not? They're not very different time periods; if either one is acceptable, both must be.
On the science side, as my results post illustrated, if you take 20-30 years to determine your trends, then changing the length doesn't change your answer much. We see this again in figure 2, where any trend computed with from 15-30 years of data gives nearly the same answer as to the current trend -- about 1.8 C per century (1.49 for 15 years, 1.79 for 20, 1.92 for 25, and 1.62 for 30 years). The figures do fluctuate some, which is to be expected. But changing from 30 to 24 years doesn't take us from a large cooling to an equally large warming, the way it can for months.
I'll probably take this up in a separate note, as it illustrates a different way of misleading yourself with graphs. For now, I'll just observe that if you compute the 10 year trends, rather than telling people to 'just look', then the most recent time there was a 10 year cooling trend was the 10 years ending with January, 1987 (with 0.03 C/century). The last time you had several months in a row where the 10 year trend to that month was a cooling was in the late 1970s -- 30 years and more back. At no time that the '10 year cooling trend' claim has been getting made, has it been true.
What's useful or interesting is that the statement itself, often linked to 'last 10 years', is not true even after allowing for substantial cherry picking. This brings us back to the interesting matter of trying to define climate. And a further reminder that if you're reading bad sources, you can't trust even the simplest of statements.
To find current temperature trends, I used the NCDC monthly temperature anomalies. The most recent month is May, 2009. To look in to current trends, then, I computed the trends from every month of the last 30 years, through to May 2009. The trend shown for January 1979 is the trend from then to May 2009. The trend for April 2009 is to May 2009. Figure 1 gives the results (actually back to 1977).

Wow, current warming trend of 120 C per century! Surely we're all going to be boiling soon? Of course not. That trend was computed from a 1 month span -- April to May of 2009. It is yet another reminder that short term variations, namely weather, can be large. It isn't climate. Climate shouldn't depend sensitively on when exactly you start your trend computation. Unfortunately that figure shows us nothing new, beyond confirming yet again (not a bad process itself, and part of the scientific approach) that weather happens, and weather variability is much larger than climate variability. So in figure 2, I zoom in a little and ignore positive trends greater than 20 C/century.

So now we can see that if someone chooses very carefully (namely, cherry picks) the starting date, they can find a cooling trend between then and May 2009 ('current'). But notice how carefully they have to choose that starting date. If it's 10 years (or any number greater than that, back to the record's start date), the trend is a warming. In fact, you can only get cooling trends occur if you choose a start date between January 2001 and January 2007 (including those months), or October, 2008. Anything farther back, or more recent, shows warming.
Both for deciding climate, and for doing science, we want our conclusions not to depend sensitively on arbitrary choices. Ending with the most recent data is not arbitrary, so we're ok there. But choosing a starting date? Science-minded folks take a figure in the range of 20-30 years, in particular 30, because over a century of experience says that 30 years is a good time period to be able to look at climate trends as opposed to weather fluctuations. i.e., not arbitrary. Choosing 2.4-8.4 years (and not 9.4, or 12, ...)? Why would we do that? Well, if we wanted to support some particular conclusion, we might do so. But that is not science.
Let's zoom our attention to the period in late 2006 through early 2007. The largest 'cooling trend' you can contrive is to start with September or October 2006, giving 3.3 C per century cooling. Of course you're flagrantly violating sensible climate practice by using 30 months instead of 30 years. But now look to April 2007, where the trend is already a warming of 3.3 C/century, and remains higher than 3.3 to the present, except for that 1 month, October 2008. If 30 months are ok for cherry pickers, why are 24 months not? They're not very different time periods; if either one is acceptable, both must be.
On the science side, as my results post illustrated, if you take 20-30 years to determine your trends, then changing the length doesn't change your answer much. We see this again in figure 2, where any trend computed with from 15-30 years of data gives nearly the same answer as to the current trend -- about 1.8 C per century (1.49 for 15 years, 1.79 for 20, 1.92 for 25, and 1.62 for 30 years). The figures do fluctuate some, which is to be expected. But changing from 30 to 24 years doesn't take us from a large cooling to an equally large warming, the way it can for months.
I'll probably take this up in a separate note, as it illustrates a different way of misleading yourself with graphs. For now, I'll just observe that if you compute the 10 year trends, rather than telling people to 'just look', then the most recent time there was a 10 year cooling trend was the 10 years ending with January, 1987 (with 0.03 C/century). The last time you had several months in a row where the 10 year trend to that month was a cooling was in the late 1970s -- 30 years and more back. At no time that the '10 year cooling trend' claim has been getting made, has it been true.
16 July 2009
Communicating Science 2
Several good comments already to the first note on this line, at Communicating Science I'd like to continue a fair amount of discussion there.
Here, I'm pulling out some of the specific suggestions folks have made for more focused discussion and elaboration. All, I'll note, are from the commentators rather than myself.
Eric asked the important question of whether I mean ideas for me, personally, or for scientists in general. I mean both. It might be a good idea for scientists to appear regularly on The Daily Show and Colbert Report. But that's probably not a good venue for me (but if John Stewart or Stephen Colbert give me a call, I'll give it a try and find out :-). Worse would be some of the anti-scientific yelling shows on TV or radio. On the other hand, I only learned about Science Cafes by accident and that's a very good venue for me. (Both that I enjoyed it, and that my host and audience did.) There probably are a lot of others.
If I read jg and eric right, in addition to blogs, educationally-oriented web sites are also something to do and have. I did work on one in the 1990s -- http://www.radix.net/~bobg/ -- but had stopped that and thought that these days blogs might be the preferred route. Certainly google gives higher scores to blogs than web sites (my blog note on sea level change shows up much higher than my sea level FAQ that's been out there, and multiply linked to, for over a decade). But what sort of organization should it have? Encyclopedia was mentioned, but I don't see much improvement from encyclopedia over blog. Neither is very organized or coherent. But maybe I'm not seeing the virtue there. Comments welcome on that, and on alternate structures you might like instead.
jg and bart mention trade/industry journals and groups. I'm not sure either what groups are meant, nor how to publish there or speak to them. The scientific societies (AMS and AGU, for instance) have in-house magazines for their members -- Bulletin of the American Meteorological Society, EOS: Transactions of the American Geophysical Union. But the audience there is already pretty knowledgeable about climate, and does routinely have articles on the topic. Plus, with about 60,000 members between them (and a lot of overlap), that seems an awfully small target.
Any suggestions on outlets to write for, groups to speak to?
And, of course, new and different thoughts are still welcome.
Here, I'm pulling out some of the specific suggestions folks have made for more focused discussion and elaboration. All, I'll note, are from the commentators rather than myself.
Eric asked the important question of whether I mean ideas for me, personally, or for scientists in general. I mean both. It might be a good idea for scientists to appear regularly on The Daily Show and Colbert Report. But that's probably not a good venue for me (but if John Stewart or Stephen Colbert give me a call, I'll give it a try and find out :-). Worse would be some of the anti-scientific yelling shows on TV or radio. On the other hand, I only learned about Science Cafes by accident and that's a very good venue for me. (Both that I enjoyed it, and that my host and audience did.) There probably are a lot of others.
If I read jg and eric right, in addition to blogs, educationally-oriented web sites are also something to do and have. I did work on one in the 1990s -- http://www.radix.net/~bobg/ -- but had stopped that and thought that these days blogs might be the preferred route. Certainly google gives higher scores to blogs than web sites (my blog note on sea level change shows up much higher than my sea level FAQ that's been out there, and multiply linked to, for over a decade). But what sort of organization should it have? Encyclopedia was mentioned, but I don't see much improvement from encyclopedia over blog. Neither is very organized or coherent. But maybe I'm not seeing the virtue there. Comments welcome on that, and on alternate structures you might like instead.
jg and bart mention trade/industry journals and groups. I'm not sure either what groups are meant, nor how to publish there or speak to them. The scientific societies (AMS and AGU, for instance) have in-house magazines for their members -- Bulletin of the American Meteorological Society, EOS: Transactions of the American Geophysical Union. But the audience there is already pretty knowledgeable about climate, and does routinely have articles on the topic. Plus, with about 60,000 members between them (and a lot of overlap), that seems an awfully small target.
Any suggestions on outlets to write for, groups to speak to?
And, of course, new and different thoughts are still welcome.
15 July 2009
What is the future of weather?
The future of weather is change. Easy enough to make that statement, but since the question brings people here periodically, let's think about it some more. I earlier mentioned the topic in Weather will still happen. Entirely true, but maybe not as helpful as it could be.
Let's go back and think about what we mean in talking about weather. Partly, it means 'not climate'. Itself also not the most helpful comment. But let's continue with both weather and climate in mind. My touchstone is "Climate is what you expect, weather is what you get." Whatever it is exactly that is happening around you right now, that's weather.
We can think a little differently and decide that our expectation -- climate -- is also part of what's happening. In that case, weather is the difference between our expectations and exactly what is going on. Since I live near Washington, DC, and it's the middle of July, I expect it to be hot. More precisely, from the Weather Underground's reports for Washington National Airport, I expect today's high to be 88 F (31 C). That's the climate for that station. If the actual high were to be 88, then as far as high temperature went, we were exactly on our climatology. Conversely, we could say that there was no 'weather' -- no difference between what we expected and what we got. It looks like the forecast for today is for the high to be 5 degrees below the climatology. So it seems more likely that we'll have 'weather' of 5 degrees cooler than normal for the high.
If we look day by day for here and other middle or high latitude locations, we'll find days that are 20-30 F warmer than usual (10-15 C), and days that are 10-15 C colder than usual. That gives us a sense of how large 'weather' is -- give or take 15 C from climatology. The figure depends on locations and seasons. In the tropics the weather variations, in terms of temperatures that is, are smaller than in the middle latitudes (if I remember correctly, 5 C, 10 F, is considered a big deviation from climatology in the tropics).
The difference between scale of weather (how many degrees away from climatology you get) in tropics and the middle or high latitudes helps us see what is happening to cause weather. In the tropics, the solar input is relatively constant day by day through the year. With similar solar inputs, you reach similar temperatures day by day, and year by year. The larger differences from climatology occur when you have some big system (large cloud bands, clusters of thunderstorms, and up to hurricanes) active. The thing which drives those big systems are temperature differences. The systems then try to flatten out the temperature differences. In low latitudes, they're more effective at this, so you see smaller variations due to weather.
Come to higher latitudes, where most people live, and you see some of those tropical systems coming up your way (hurricanes, typhoons, etc.) carrying that very warm, very moist air -- replacing the more moderate air 'native' to your location. Or, here in the mid-latitudes, wait a bit and get a wave of cold air coming down from the colder higher latitudes. On top of both, you have the fact that the amount of sun you get varies by a lot through the course of a year. If the only thing happening were the change in solar input, we could calculate the temperatures, and temperature changes, we'd expect (a climate estimate) using the simplest climate model.
Now let climate change enter the picture. Will it change the fact that solar input varies little in the tropics and tremendously at the poles? No. Will it change the fact that far more solar input is in the tropics than in middle latitudes? No. Will it change the fact that weather systems respond to temperature differences across the planet by trying to smooth out those differences? No.
Since the answers to all those (and a host of others that are related) is no, weather will still happen. A little more detailed:
we'll still see days/weeks/months, even years, where the temperatures run below normal.
we'll also still see temperatures run above normal.
In the mid-latitudes, those differences on a daily basis will still be 10-15 C (20-30 F)
Now an application of climate change to our daily observations. Let's say (to keep the numbers easy) that the climate change of the last century were a 2 F (1 C) warming at my location. Before that warming occurred, the expected high would have been 86 F. Our actual high of 83 F represents 'weather' of 3 degrees F below the former normal. Given the current, warmer, climate, it means today's weather is 5 F below normal. Anything odd about 5 F off normal for a day? Hardly. The record low is 15 F below the average low, the record high is 12 F above the average high. (Tamer numbers here than I quoted above because a) it's summer and the ranges are smaller and b) I'm more knowledgeable about the weather for Chicago, which is more variable than DC.)
Weather will still happen, and have similar magnitudes to the past. What changes, as climate changes, is the average and some more subtle figures. They'll be the subject of their own note later.
Let's go back and think about what we mean in talking about weather. Partly, it means 'not climate'. Itself also not the most helpful comment. But let's continue with both weather and climate in mind. My touchstone is "Climate is what you expect, weather is what you get." Whatever it is exactly that is happening around you right now, that's weather.
We can think a little differently and decide that our expectation -- climate -- is also part of what's happening. In that case, weather is the difference between our expectations and exactly what is going on. Since I live near Washington, DC, and it's the middle of July, I expect it to be hot. More precisely, from the Weather Underground's reports for Washington National Airport, I expect today's high to be 88 F (31 C). That's the climate for that station. If the actual high were to be 88, then as far as high temperature went, we were exactly on our climatology. Conversely, we could say that there was no 'weather' -- no difference between what we expected and what we got. It looks like the forecast for today is for the high to be 5 degrees below the climatology. So it seems more likely that we'll have 'weather' of 5 degrees cooler than normal for the high.
If we look day by day for here and other middle or high latitude locations, we'll find days that are 20-30 F warmer than usual (10-15 C), and days that are 10-15 C colder than usual. That gives us a sense of how large 'weather' is -- give or take 15 C from climatology. The figure depends on locations and seasons. In the tropics the weather variations, in terms of temperatures that is, are smaller than in the middle latitudes (if I remember correctly, 5 C, 10 F, is considered a big deviation from climatology in the tropics).
The difference between scale of weather (how many degrees away from climatology you get) in tropics and the middle or high latitudes helps us see what is happening to cause weather. In the tropics, the solar input is relatively constant day by day through the year. With similar solar inputs, you reach similar temperatures day by day, and year by year. The larger differences from climatology occur when you have some big system (large cloud bands, clusters of thunderstorms, and up to hurricanes) active. The thing which drives those big systems are temperature differences. The systems then try to flatten out the temperature differences. In low latitudes, they're more effective at this, so you see smaller variations due to weather.
Come to higher latitudes, where most people live, and you see some of those tropical systems coming up your way (hurricanes, typhoons, etc.) carrying that very warm, very moist air -- replacing the more moderate air 'native' to your location. Or, here in the mid-latitudes, wait a bit and get a wave of cold air coming down from the colder higher latitudes. On top of both, you have the fact that the amount of sun you get varies by a lot through the course of a year. If the only thing happening were the change in solar input, we could calculate the temperatures, and temperature changes, we'd expect (a climate estimate) using the simplest climate model.
Now let climate change enter the picture. Will it change the fact that solar input varies little in the tropics and tremendously at the poles? No. Will it change the fact that far more solar input is in the tropics than in middle latitudes? No. Will it change the fact that weather systems respond to temperature differences across the planet by trying to smooth out those differences? No.
Since the answers to all those (and a host of others that are related) is no, weather will still happen. A little more detailed:
we'll still see days/weeks/months, even years, where the temperatures run below normal.
we'll also still see temperatures run above normal.
In the mid-latitudes, those differences on a daily basis will still be 10-15 C (20-30 F)
Now an application of climate change to our daily observations. Let's say (to keep the numbers easy) that the climate change of the last century were a 2 F (1 C) warming at my location. Before that warming occurred, the expected high would have been 86 F. Our actual high of 83 F represents 'weather' of 3 degrees F below the former normal. Given the current, warmer, climate, it means today's weather is 5 F below normal. Anything odd about 5 F off normal for a day? Hardly. The record low is 15 F below the average low, the record high is 12 F above the average high. (Tamer numbers here than I quoted above because a) it's summer and the ranges are smaller and b) I'm more knowledgeable about the weather for Chicago, which is more variable than DC.)
Weather will still happen, and have similar magnitudes to the past. What changes, as climate changes, is the average and some more subtle figures. They'll be the subject of their own note later.
14 July 2009
Communicating Science
There seems to be a small industry these days, consisting of telling us that scientists either or both a) are bad communicators and b) should be doing more communicating with the general public. The latest round is spurred by the articles from Chris Mooney and Sheril Kirshenbaum appearing in many venues as part of promotion for their book Unscientific America. (You can track some of it, in between the feud with PZ Myers, at their blog The Intersection and the articles they reference.)
I confess some amusement at being told both that I (as a scientist) am both bad at something, and should be doing it more. Unless it's something for my own entertainment (singing in the car, for instance), or health (running), I generally avoid doing things that I'm bad at. And think that most people are similar in that approach. But that's an aside to the more important matter.
The continual failing, including from the current round of Mooney and Kirshenbaum articles, is that they (and others making similar comments) never do get around to telling us (scientists) just what it is we should do differently, nor where we should be doing it. Fine-sounding words are mentioned, like 'reach out more'. But, let's try to carry that out. Er. What does it mean after all? Reach out more sounds nice, but after reading The Intersection for quite some time, and asking this question routinely, I still don't know what they mean. I do know that they've written routinely that scientist blogs are not the answer, so my efforts here are a waste by their lights. That's fine, their opinion. (Though I still wonder what, exactly, the question is.)
So I'll turn the question to my gentle, and not-so gentle, readers and ask you for what _you_ would like to see scientists (me as an example) do more of. And, what you'd like to see less of. More blog posts, fewer but better-crafted, more scientists writing blogs, drop the blogs and write letters to the editor, buy TV time and make science-o-mercials, ...?
In like vein, what are some of the dos and don'ts about communication you'd suggest? I do make some effort, for instance, to use a more common vocabulary and avoid math. But ... I do still use math, and know (following the quote from Stephen Hawking, who was advised when writing Brief History of Time that each equation would halve his sales) that this isn't the thing to do for widest readership. Even better if you can point to examples of good, and bad, ideas that I've carried out (intentionally or not) in the blog here.
I confess some amusement at being told both that I (as a scientist) am both bad at something, and should be doing it more. Unless it's something for my own entertainment (singing in the car, for instance), or health (running), I generally avoid doing things that I'm bad at. And think that most people are similar in that approach. But that's an aside to the more important matter.
The continual failing, including from the current round of Mooney and Kirshenbaum articles, is that they (and others making similar comments) never do get around to telling us (scientists) just what it is we should do differently, nor where we should be doing it. Fine-sounding words are mentioned, like 'reach out more'. But, let's try to carry that out. Er. What does it mean after all? Reach out more sounds nice, but after reading The Intersection for quite some time, and asking this question routinely, I still don't know what they mean. I do know that they've written routinely that scientist blogs are not the answer, so my efforts here are a waste by their lights. That's fine, their opinion. (Though I still wonder what, exactly, the question is.)
So I'll turn the question to my gentle, and not-so gentle, readers and ask you for what _you_ would like to see scientists (me as an example) do more of. And, what you'd like to see less of. More blog posts, fewer but better-crafted, more scientists writing blogs, drop the blogs and write letters to the editor, buy TV time and make science-o-mercials, ...?
In like vein, what are some of the dos and don'ts about communication you'd suggest? I do make some effort, for instance, to use a more common vocabulary and avoid math. But ... I do still use math, and know (following the quote from Stephen Hawking, who was advised when writing Brief History of Time that each equation would halve his sales) that this isn't the thing to do for widest readership. Even better if you can point to examples of good, and bad, ideas that I've carried out (intentionally or not) in the blog here.
Subscribe to:
Posts (Atom)


